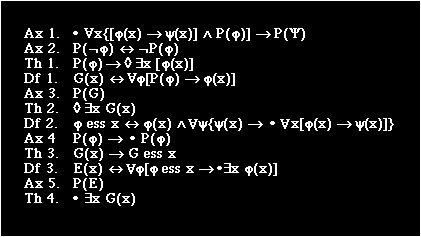
Voi olla, että rajallinen kallon sisälle sidottu tajunta ei yksinkertaisesti pysty ajattelulla ymmärtämään, mitä ääretön on. Voi olla niinkin, että "ääretön" on perin juurin viallinen käsite, itseensä sidotun ymmärryksen luoma abstraktio, jolla ei ole mitään tekemistä ympäröivän todellisuuden kanssa, kuin vangin houre siitä millaista vapaudessa on. Ehkä "ääretön" on tieteen eskapismia. Jokainen joka on vakavissaan tekemisissä äärettömyyden käsitteen kanssa, paukuttelee tieteen rajoja. Tiedehän odottaa, että asiantilojen on oltava mitattavissa ja mittaukset olisi oltava toistettavissa. Nykyisessä matematiikassa hyväksytään, että äärettömyyden käsitteitä on olemassa ääretön määrä, ja jopa äärettömän monella tavalla ääretön määrä.

Reippaita yrityksiä äärettömyyden mittaamiseksi on silti tehty. Georg Cantor (1845-1918) käytti välineenään joukko-oppia. Hänen onnistui todistaa algebralla, että äärettömän suuri joukko voi olla yhtä mahtava kuin sen aito osajoukko. Hän tuli hulluksi. Häntä seurasi Kurt Gödel (1906-1978), joka todisti, että matematiikkaan sisältyy aksioomia, joita ei milloinkaan voida todistaa. Hänkin tuli hulluksi.

Matematiikka sanoo sanatarkasti "Äärettömien joukkojen mahtavuutta tarkastellessaan Cantor havaitsi, että kaikkien äärettömien joukkojen mahtavuuden ei tarvitse olla sama, toisin kuin häntä ennen oli ajateltu. Cantor onnistui osoittamaan, että esim. reaalilukujen joukko (R) on mahtavampi kuin luonnollisten lukujen joukko (N). Cantorin tuloksista seuraa, että kaikki reaaliluvut eivät ole algebrallisia. Ei-algebrallisia reaalilukuja (ja kompleksilukuja) sanotaan transkendenttiluvuiksi. Jonkin aikaa olikin ongelmana, että näitä lukuja tiedettiin olevan olemassa, mutta niitä ei heti onnistuttu konstruoimaan."

Kun Cantor näin oli saanut selville, että on olemassa joukko lukuja, joista emme tiedä, miten niihin päästään, kävi selväksi, että joukko-opissa on parannettavaa. Brittiläisellä huumorintajulla varustettu yhtä ja toista aikaan saanut Bertrand Russell kuvasi ongelman Russellin paradoksissa: Oletetaan joukko, jonka alkioina ovat ne joukot, jotka eivät ole itsensä alkioita. Tällöin kyseinen joukko on itsensä alkio jos ja vain jos se ei ole itsensä alkio.

Hassua kyllä, Georg Cantor, joka oli itse vakuutellut että "Matematiikassa kysymyksenasettelun taito on arvokkaampi kuin vastausten löytäminen", ei nähnyt tässä mitään hauskaa. Hän tuli hulluksi ja kuoli mielisairaalassa.

Kurt Gödel kävi selvittämään Cantorin löytämää ongelmavyyhteä ja tarjosi ratkaisuksi transfiniittisiä lukuja ja ennen kaikkea kuuluisan epätäydellisyysteoreeman vuonna 1931: Aksiomaattista järjestelmää (= rakennelmaa, johon sisältyy perusoletuksia, joita ei voida kyseenalaistaa) ei voida osoittaa ristiriidattomaksi sen omista aksioomista lähtien. Eipä tietenkään, mutta tätäkään ilmeisesti kukaan ei ollut paperilla todistanut ennen kuin Gödel osoitti näin olevan. Täydellinen todistaminen onnistuisi vain hyvin laajassa järjestelmässä, jota puolestaan ei voida osoittaa ristiriidattomaksi, koska mahdollisia todistettavia on, niin, ääretön määrä. Tämä tulos merkitsi kuoliniskua toiveille saada matematiikka varmasti ristiriidattomaksi aksiomatisoimalla se perusteellisesti.

Realistisen koulukunnan edustaja Leopold Kronecker, joka oli soimannut ankarasti Georg Cantoria, hyökkäsi myös Kurt Gödeliä vastaan, kun tämä esitteli ajatuksensa transfiniittisistä luvuista. Kronecker yritti estää jopa Gödelin tutkielman julkaisemisen. Kroneckerin mielestä hänen entinen oppilaansa Cantor oli "tieteellinen silmänkääntäjä", "rappio-olento" ja "nuorison turmelija". Gödel ei ollut yhtään parempi. Kroneckerin mielestä transfiniittisiä lukuja ei ole olemassakaan, vaan "Kokonaisluvut on hyvä Jumala tehnyt, kaikki muu on ihmistyötä".

Tässä nuorisoa turmelevia ja villitseviä lauseita, jotka ilmeisesti myös ovat jumalanpilkkaa:  

m on transfiniittinen kardinaaliluku
m + 1 = m
(N)0 =< m
ei ole olemassa kardinaalilukua n, jossa (N)0 + n = m

Hassua kyllä, Kurt Gödel, Einsteinin ystävä ja "suurin loogikko Aristoteleen jälkeen", meni järjiltään ja eli loppuelämänsä hermoparantoloissa. Cantorin tavoin vanha Gödel tuli vainoharhaiseksi, epäili että häntä vastaan on perustettu salaliitto ja että hänet yritetään myrkyttää. Myrkytyksen pelossa Gödel ei uskaltanut syödä ja hän käytännössä kuoli nälkään. Kuollessaan hän painoi vain 39 kiloa.

Gödelin epätäydellisyysteoreemassa on myöhemmin nähty todistus milloin mistäkin. Se vaikuttaa maailman käyttökelpoisimmalta ja merkityksellisimmältä väittämältä, joka kuulemma todistaa Jumalan olemassaolon, mahdollistaa aikamatkustuksen, selittää Raamatun, ja on USA:n perustuslain tieteellinen perusta. Tämä on oikein mainiota.

Onneksi Gödel antoi seuraajilleen käytännön ohjeet siitä, kuinka äärettömyyttä on tutkittava:
i) Ensin on suljettava muut aistit esimerkiksi makaamalla hiljaisessa paikassa. Tällaisen negatiivisen toiminnan toteuttaminen ei kuitenkaan riitä, vaan samalla on etsittävä aktiivisesti mielensä avulla.
ii) On virhe antaa jokapäiväisen todellisuuden asettaa ehtoja mahdollisuudelle ja kuvitella vain fysikaalisten objektien yhdistymisiä ja permutaatioita; mieli kykenee havaitsemaan suoraan äärettömiä joukkoja.
iii) Tällaisen ajattelun ja koko filosofian lopullinen päämäärä on Absoluuttisen ymmärtäminen.

Kun lasketaan yhteen traskendentaalinen mietiskely ja konstruktioiden todistaminen konstruktioiksi, joiden perustaa ei voi liikuttaa ilman että konstruktiot hajoavat, päästään helposti John D. Barrow'n kuvaamaan tilanteeseen: "Jos uskonto määriteltäisiin ajattelumalliksi johon sisältyy todistamattomia lauseita, niin Gödel ei ainoastaan ole osoittanut matematiikkaa uskonnoksi, vaan peräti ainoaksi uskonnoksi, joka kykenee todistamaan olevansa sellainen."

Gödelistä oppineesti ja selkeästi kirjoittanut Juha Lehrbäck (kts. viite) näkee Barrow'n lausumassa sarkasmia. Maallikko ihmettelee miksi. Mutta sarkasmi, ironia ja satiiri ovat ehdottomasti hyviä asioita. Myrkyllistä satiirikkoa on hyödytöntä yrittää myrkyttää.  

http://www.cc.jyu.fi/~juhaleh/godel.html
http://www.tsv.fi/ttapaht/998/pekonen.htm
http://en.wikipedia.org/wiki/Transfinite_numbers